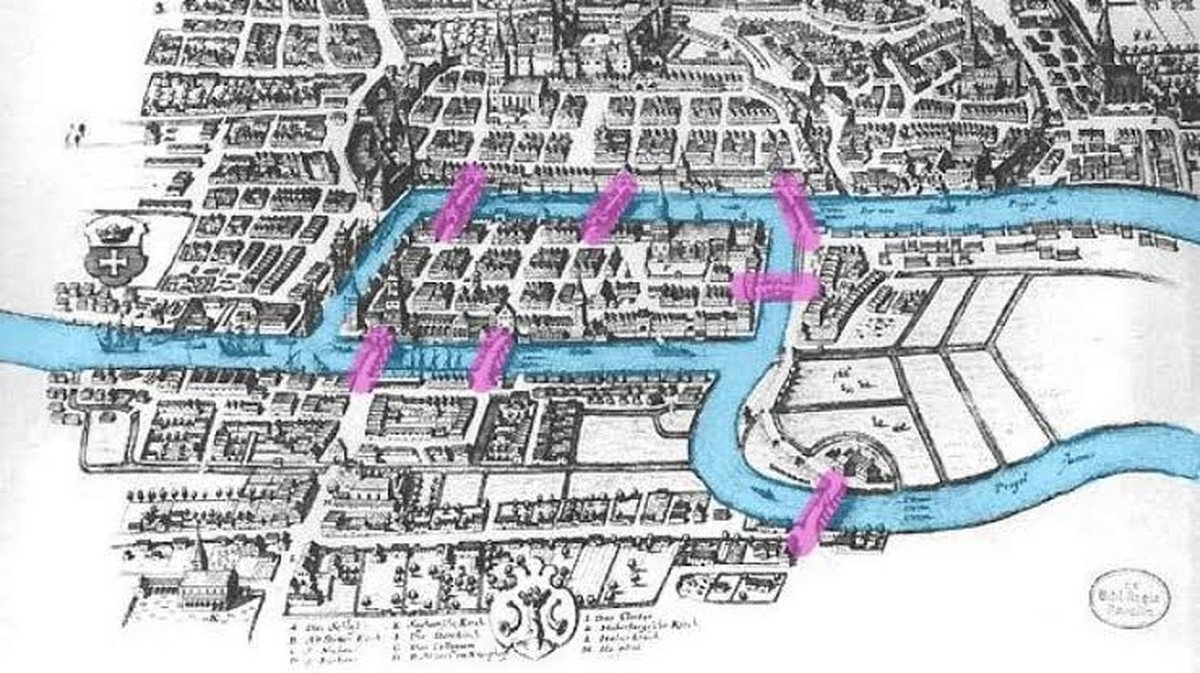
Město Pruska zvané Königsberg (dnes Kaliningrad v Rusku) bylo rozděleno řekou Pregel a spojeno sedmi mosty, které unifikovaly dvě ostrovy a protilehlé břehy. Město tak bylo rozděleno do čtyř zón. Mezi místními obyvateli kolovala legenda o podivuhodné zábavě: nalezení cesty, která by vedla přes všechny mosty právě jednou. Zdařilé provedení této jednoduché úlohy se však ukázalo jako nemožné.
Otázka byla předána matematikovi Leonhardu Eulerovi. Zprvu Eulero nebyl přesvědčen, že by se jednalo o skutečný matematický problém. Avšak při pohledu na mapu města měl klíčový pohled: nezáleželo na tom, jakým způsobem se pohybovalo mezi čtyřmi zónami města (označenými jako A, B, C a D), ale pouze na pořadí, v jakém byly mosty překračovány.
Tímto způsobem dospěl k brilantnímu zjednodušení: zobrazit pozemky jako body a mosty jako čáry. Můžeme tedy problém zjednodušit následovně:
Nevědomky Eulero vytvářel základy nové disciplíny, teorie grafů, která je dodnes klíčová pro studium schémat, jež mohou být redukovaná na prvky a propojení.
Graf je jednoduchý způsob, jak reprezentovat spojení: skládá se z bodů (nazývaných uzly) a čar, které tyto body spojují (nazývaných hrany). Při analýze systému zjistil, že možnost překonat všechny mosty právě jednou závisí výlučně na počtu čar, které „se dotýkají“ každého bodu, tj. na stupni uzlů. Takovýto typ cesty – dnes nazývané eulerovská cesta – je možný pouze za těchto podmínek:
- všechny uzly mají sudý stupeň (tj. sudý počet čar spojených s bodem), nebo
- přesně dva uzly mají lichý stupeň (výchozí a cílový bod).
Problém? V Königsbergu měly všechny čtyři uzly lichý stupeň. Jinými slovy, městská výzva byla od začátku nemožná.
Že by to byla ironie? Jediný způsob, jak učinit tento problém řešitelný, by bylo skartovat alespoň jeden z mostů. Což se nakonec skutečně stalo, avšak tragicky: během druhé světové války byla část města a některé mosty zničeny bombardováním, než byl Königsberg přetvořen na dnešní Kaliningrad.
Nicméně Eulerovo řešení přežilo daleko déle než původní mosty. Tento jednoduchý městský rébus dal podnět vzniku teorie grafů a obecně novému způsobu uvažování o tvarech a spojeních, což otevřelo cestu k moderní topologii.